のコツ!終わらない人続出?例題・練習問題と解答付き!のアイキャッチ画像-304x160.png)
玉手箱の計数理解(非言語・数学)は数多くあるWEBテスト(適性検査)の中でもかなり難しい科目です。
※「玉手箱とは?対策方法や試験の特徴は?対策いらない?完全解説で就活生・社会人必見!」もぜひ参考にしてください。
なので、事前にしっかりと勉強・対策をしておかないと壊滅的な点数になる可能性が高いのでご注意ください。
本記事では玉手箱の受検回数=100回超・日本一玉手箱に詳しい私アキラが、玉手箱の計数理解(非言語・数学)のコツについて例題を使いながら解説していきます。
また、計数の問題がすべて解き終わらない人はどうするべきかや電卓は使えるのかなどについても解説します。
最後には計数の練習問題もご用意しているので、ぜひ最後までお読みください。
ちなみにですが、玉手箱にはたった3時間の勉強で玉手箱が通過してしまう勉強法があります。
これさえあれば限りなく少ない努力で内定に大きく近づきます。
これは私が100回以上もの玉手箱受検を通して生み出した、どの本にも載っていない超コスパの良い究極の勉強法です。
興味のある人はぜひ以下のボタンからその方法をチェックしてみてください。
目次
玉手箱の計数理解(非言語・数学)の例題
玉手箱の計数理解(非言語・数学)では以下の3科目が用意されています。
- 図表の読み取り(35分で40問または15分で29問)
- 表の空欄の推測(35分で35問または20分で20問)
- 四則逆算(9分で50問)
※「玉手箱の計数35分はどっち?見分ける方法3つをご紹介!」もぜひ合わせてご覧ください。
まずはそれぞれの例題を見ていきましょう。
図表の読み取り
計数の図表の読み取りは与えられた図や表をもとにして必要な情報を読み取り、用意された設問に答える問題です。
以下10パターンの問題が用意されています。
- 割合
- 割合の比較
- 増減率
- 数量
- 平均
- 比
- 文字式
- 正誤選択
- 少し変わった図表の問題
- 選択肢に「わからない」が登場する問題
それぞれの例題は以下の通りです。
※「玉手箱の問題・例題を全科目紹介!練習問題も無料!どんな問題か知りたい人必見」もぜひ参考にしてください。
1:割合
割合は、2つの数値を比較して何倍か?や何%か?を求める問題です。
【例題】
以下の表を見て問いに答えなさい。
<K電子工業>
| 単位:100万ドル | 国内売上額 | 海外売上額 |
|---|---|---|
| 1月 | 12,589 | 4,910 |
| 2月 | 19,503 | 4,791 |
| 3月 | 23,485 | 6,310 |
| 4月 | 28,593 | 7,499 |
| 5月 | 19,296 | 5,921 |
| 6月 | 22,332 | 5,430 |
| 7月 | 22,204 | 7,593 |
| 8月 | 27,001 | 8,503 |
| 9月 | 38,947 | 8,862 |
| 10月 | 49,394 | 14,580 |
5月の総売上額に占める国内売上額の割合は、9月のそれのおよそ何倍か。最も近いものを以下の選択肢の中から1つ選びなさい。
- 0.7倍
- 0.9倍
- 1.0倍
- 1.1倍
- 1.3倍
【解答&解説】
5月の総売上額は19,296+5,921=25,217です(単位は省略します)
よって、5月の総売上額に占める国内売上額の割合は19,296÷25,217×100≒76.52[%]です。
同様に考えて、9月の総売上額は38,947+8,862=47,809です。
よって、9月の総売上額に占める国内売上額の割合は38,947÷47,809×100≒81.46[%]です。
以上より、76.52÷81.46=0.939・・・となるので、正解は0.9倍・・・(答)です。
🔽 本にも載ってない極秘情報 🔽
2:割合の比較
割合の比較は、割合の増減や、どの割合が最も大きいか?など、割合同士を比較する問題です。
【例題】
以下の図表を見て、次の問いに答えなさい。
<法人経営体数の変化>
| 農業組合法人 | 会社 | 各種団体 | その他 | 合計 | |
|---|---|---|---|---|---|
| 2000年 | 1,341 | 3,446 | 309 | 176 | 5,272 |
| 2005年 | 1,663 | 6,016 | 643 | 378 | 8,700 |
| 2010年 | 3,077 | 8,395 | 652 | 387 | 12,511 |
| 2014年 | 4,600 | 9,400 | 700 | 600 | 15,300 |
全体の法人数に対する農業組合法人の割合について、前の年から最も上昇した年はおそよ何%上昇したか。最も近いものを、以下の選択肢から1つ選びなさい。
- 4.5%
- 5.0%
- 5.5%
- 6.0%
- 6.5%
【解答&解説】
各年における全体の法人数に対する農業組合法人の割合は以下の通りです。
- 2000年:1,341÷5,272×100≒25.44[%]
- 2005年:1,663÷8,700×100≒19.11[%]
- 2010年:3,077÷12,511×100≒24.59[%]
- 2014年:4,600÷15,300×100≒30.07[%]
前の年に比べて割合が上昇しているのは、2010年と2014年です。
- 2010年の上昇率=24.59-19.11≒5.5[%]
- 2014年の上昇率=30.07-24.59≒5.5[%]
なので、正解は5.5%・・・(答)となります。
3:増減率
増減率は、基準と比べて増加した割合や減少した割合を求める問題です。
【例題】
図表を見て次の問いに答えなさい。
<D社の売上額、従業者数、事業所数の推移>
| 年 | 売上額(百万円) | 従業者数(人) | 事業所数 |
|---|---|---|---|
| 2013 | 9,868,530 | 164,891 | 2,728 |
| 2014 | 10,754,392 | 166,823 | 2,431 |
| 2015 | 9,912,248 | 160,277 | 2,056 |
| 2016 | 11,034,521 | 152,093 | 1,997 |
| 2017 | 12,956,167 | 146,998 | 1,980 |
| 2018 | 12,802,445 | 143,802 | 1,937 |
従業者1人あたりの売上額において、2016年から2018年までの増加率は、2013年から2015年までの増加率と比べておよそ何%増加したか。最も近いものを、以下の選択肢から1つ選びなさい。
- 17%
- 19%
- 21%
- 22%
- 25%
【解答&解説】
2013年、2015年、2016年、2018年の従業者1人あたりの売上額は以下の通りです。
- 2013年:9,868,530÷164,891≒59.85
- 2015年:9,912,248÷160,277≒61.84
- 2016年:11,034,521÷152,093≒72.55
- 2018年:12,802,445÷143,802≒89.03
よって、
- 2016年から2018年までの増加率=(89.03÷72.55-1)×100≒22.7[%]
- 2013年から2015年までの増加率=(61.84÷59.85-1)×100≒3.3[%]
となるので、22.7-3.3=19.4より、正解は19%・・・(答)となります。
4:数量
数量は、総数や総額、人数の割合などの様々な数量を求める問題です。
【例題】
図表を見て、次の問いに答えなさい。
<ドラッグストアの売上高と店舗数の推移>
| 年 | 売上高(百万円) | 店舗数(店) |
|---|---|---|
| 2010 | 8,482,701 | 45,769 |
| 2012 | 9,380,512 | 50,206 |
| 2014 | 10,459,716 | 55,774 |
| 2016 | 10,832,003 | 57,818 |
| 2018 | 11,261,655 | 58,340 |
2018年と2010年のドラッグストアの売上高の差額はおよそ何億円か。最も近いものを、以下の選択肢から1つ選びなさい。
- 27億円
- 277億円
- 2,779億円
- 27,790億円
- 277,900億円
【解答&解説】
11,261,655-8,482,701=2,778,954(百万円)なので、正解は27,790億円・・・(答)となります。
5:平均
平均は、ある数とある数の平均を求めたり、平均同士を比べたりする問題です。
【例題】
図表を見て次の問いに答えなさい。
<映画の総興行収入>
| 2001年 | 2002年 | 2003年 | 2004年 | 2005年 | |
|---|---|---|---|---|---|
| 日本映画 | 78,144 | 53,294 | 67,125 | 79,054 | 81,780 |
| 海外映画 | 122,010 | 143,486 | 136,134 | 131,860 | 116,380 |
| 合計 | 200,154 | 196,780 | 203,259 | 210,914 | 198,160 |
1年あたりの平均興行収入について、海外映画は日本映画の何倍か。最も近いものを、以下の選択肢から1つ選びなさい。
- 0.7倍
- 1.2倍
- 1.5倍
- 1.8倍
- 2.1倍
【解答&解説】
日本映画の平均興行収入は、(78,144+53,294+67,125+79,054+81,780)÷5=71,879.4です。
同様に、海外映画の平均興行収入は、(122,010+143,486+136,134+131,860+116,380)÷5=129,974です。
129,974÷71,879.4=1.80822・・・となるので、答えは1.8倍・・・(答)となります。
🔽 本にも載ってない極秘情報 🔽
6:比
比は、一方を1や100としたときに、もう一方がいくつで表せるかを求める問題です。
【例題】
図表を見て次の問いに答えなさい。
| 国 | 人口(百万人) | 面積(万平方キロメートル) |
|---|---|---|
| 日本 | 125.5 | 37.7 |
| アメリカ | 331.9 | 983.3 |
| ロシア | 143.4 | 1709.8 |
日本の人口を100とすると、アメリカの人口は、およそいくつで表されるか。最も近いものを、以下の選択肢から1つ選びなさい。
- 24
- 26
- 246
- 264
- 2460
【解答&解説】
331.9÷125.5×100=264.46・・・なので、答えは264・・・(答)となります。
7:文字式
文字式は、一方をXなどの文字にしたときに、もう一方が何Xと表せるかを求める問題です。
【例題】
図表を見て次の問いに答えなさい。
| 都道府県 | 人口(万人) | 面積(平方キロメートル) |
|---|---|---|
| 栃木 | 191 | 6,408 |
| 千葉 | 627 | 5,157 |
| 東京 | 1,404 | 2,194 |
栃木の1平方キロメートルあたりの人口密度をXとしたとき、東京の1平方キロメートルあたりの人口密度、どのように表されるか。最も近いものを、以下の選択肢から1つ選びなさい。
- 15.3X
- 18.3X
- 19.4X
- 20.4X
- 21.3X
【解答&解説】
人口密度=人口÷面積です。
栃木と東京の1平方キロメートルあたりの人口密度は以下の通りです。
- 栃木:191÷6,408=0.0298≒300人
- 東京:1,404÷2,194=0.6399≒6,400人
6,400÷300=21.3・・・なので、答えは21.3X・・・(答)となります。
8:正誤選択
正誤選択は、図表から正しいと判断できる選択肢を選ぶ問題です。手間がかかる問題が多いので、時間がない人は飛ばしても良い問題となります。
【例題】
図表を見て次の問いに答えなさい。
<農産物の全国平均販売価格の推移>
| 単位(kg) | 2017年(円) | 2018年(円) | 2019年(円) | 2020年(円) | 2021年(円) | |
|---|---|---|---|---|---|---|
| 小麦 | 60 | 1,927 | 2,513 | 2,457 | 2,595 | 2,829 |
| 白米 | 10 | 3,495 | 3,518 | 3,560 | 3,540 | 3,333 |
| 大豆 | 60 | 7,577 | 6,907 | 7,733 | 8,899 | 8,665 |
| なす | 5 | 1,621 | 1,726 | 1,605 | 1,720 | 1,541 |
| キャベツ | 10 | 744 | 881 | 624 | 725 | 520 |
表から明らかに正しいと言えるものを、以下の選択肢から1つ選びなさい。
- 2020年における1kgあたりの全国平均販売価格が最も高いのは大豆である。
- 2019年から2020年にかけては、どの農産物も全国平均販売価格が増加している。
- 2021年における大豆の1kgあたりの全国平均販売価格は、2021年における小麦の1kgあたりの全国平均販売価格の約4倍である。
- 2017年から2018年にかけての全国平均販売価格の増加率は、なすよりもキャベツの方が大きい。
- 2021年の白米の全国平均販売価格は、2018年の白米の全国平均販売価格よりも10%減少した。
【解答&解説】
1:2020年における1kgあたりの全国平均販売価格は、大豆の8,899÷60より、大豆の上にある白米の3,540÷10の方が明らかに数値が大きくなります。よって、1は正しくありません。
2:2019年から2020年にかけて、白米の全国平均販売価格は減少しています。よって、2は正しくありません。
3:2021年における大豆と小麦の1kgあたりの全国平均販売価格を求めてみます。
- 大豆:8,665÷60≒144.4[円]
- 小麦:2,829÷60≒47.15[円]
144.4÷47.15≒3.06[倍]なので、2021年における大豆の1kgあたりの全国平均販売価格は、2021年における小麦の1kgあたりの全国平均販売価格の約3倍であることがわかります。よって、3は正しくありません。
4:2017年から2018年にかけてのなすとキャベツの全国平均販売価格の増加率は以下の通りです。
- なす:1,726÷1,621×100-100≒6.477[%]
- キャベツ:881÷744×100-100≒18.41[%]
よって、4は正しいことがわかるので、正解は4・・・(答)です。
5:2018年から2021年にかけての白米の全国平均販売価格の増加率は、3,333÷3,518×100-100≒-5.258[%]です。
よって、5は正しくないことがわかります。
9:少し変わった図表の例題
以下の表を見て問いに答えなさい。
<山陽新幹線の主要駅間の距離表(単位:km)>
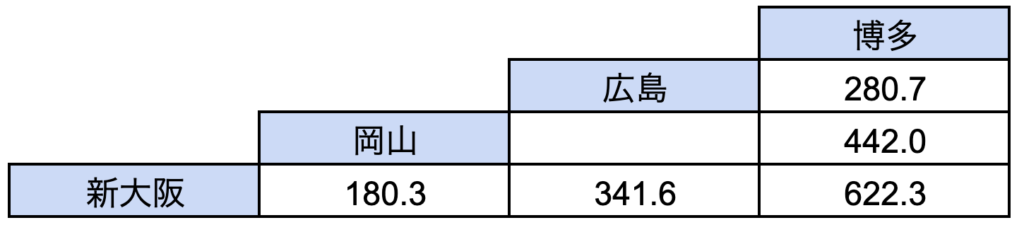
岡山ー広島間は何kmか。以下の選択肢の中から1つ選びなさい。
- 60.9km
- 100.4km
- 161.3km
- 180.3km
- 261.7km
【解答&解説】
例えば表中の180.3kmは新大阪と岡山の距離を表しています。
同様に、341.6kmは新大阪と広島の距離を表しています。
岡山ー広島の距離は新大阪ー広島の距離から新大阪ー岡山の距離を引くことで求めることが可能です。
よって、正解は341.6-180.3=161.3[km]・・・(答)となります。

10:選択肢に「わからない」が登場する問題
こちらは、その名の通り、選択肢に「わからない」が登場する問題です。
【例題】
図表を見て次の問いに答えなさい。
<産業別就業者数の推移>
| 年 | 第一次産業(万人) | 第二次産業(万人) | 第三次産業(万人) |
|---|---|---|---|
| 1995年 | 385 | 1,994 | 4,000 |
| 2000年 | 321 | 1,839 | 4,067 |
| 2005年 | 298 | 1,596 | 4,142 |
| 2010年 | 238 | 1,412 | 3,965 |
| 2015年 | 222 | 1,392 | 3,961 |
2008年の第二次産業の就業者数は何人か。以下の選択肢から1つ選びなさい。
- 1,574万人
- 1,532万人
- 1,459万人
- 1,442万人
- グラフからはわからない
【解答&解説】
グラフには、2008年の第二次産業の就業者数についての情報がないため、正解はグラフからはわからない・・・(答)となります。
🔽 本にも載ってない極秘情報 🔽
表の空欄の推測
表の空欄の推測は表の数値から法則性を見つけ、空欄に入る数値を推測する問題です。
玉手箱の計数の科目で一番難しいので必ず対策しておきましょう。
※「玉手箱は難しいので要注意!3時間の勉強で通過する極秘裏ワザをご紹介」もぜひ合わせてご覧ください。
表の空欄の推測では以下7パターンの問題が出題されます。
- 比例
- 大小
- 算出式
- 推移
- 合計が同じ
- 積算
- 列ごとに計算
それぞれの例題は以下です。
1:比例
比例は、「ある項目が別の項目の何倍」という比例関係にあるものです。
【例題】
あるレストランでワインの販売量を集計しています。
<ワインの販売量>
| 5月1日 | 5月2日 | 5月3日 | 5月4日 | 5月5日 | |
|---|---|---|---|---|---|
| 降水確率[%] | 50 | 80 | 20 | 15 | 45 |
| 平均気温[℃] | 21 | 21 | 21.5 | 21 | 21.5 |
| 販売量[L] | 200 | 140 | 260 | 270 | ? |
5月5日のワインの販売量は何Lと推測できるか。
- 210L
- 230L
- 260L
- 270L
- 280L
【解答&解説】
- 降水確率が10%上がるごとに、ワインの販売量は20L減少
- 降水確率が10%下がるごとに、ワインの販売量は20L増加
という法則性を見つけられるかどうかです。
例えば、5月2日から5月3日にかけては降水確率が80-20=60[%]下がっています。
よって、ワインの販売量は5月2日から5月3日にかけて6×20=120[L]増加しています。
※140+120=260より、5月3日のワインの販売量は確かに260Lになっていることが確認できます。
5月4日から5月5日にかけては降水確率が45-15=30[%]上がっているので、ワインの販売量は60L減少するはずです。
よって、正解は270-60=210[L]・・・(答)となります。
2:大小
大小は、「ある項目が大きいものほど、別の項目が小さい」といった大小関係から、当てはまる選択肢を1つに絞り込めるものです。
【例題】
ある研究所で、インフルエンザに感染する確率を調査しています。
| A班 | B班 | C班 | D班 | E班 | F班 | |
|---|---|---|---|---|---|---|
| 平均年齢(歳) | 32 | 28 | 24 | 20 | 23 | 26 |
| 湿度(%) | 40 | 40 | 40 | 60 | 60 | 60 |
| 温度(℃) | 16 | 16 | 16 | 16 | 16 | 16 |
| 接触時間(分) | 10 | 20 | 30 | 10 | 20 | 30 |
| 感染確率(%) | 7 | ? | 15 | 4 | 8 | 12 |
B班でインフルエンザに感染する確率は何%と推測できるか。
- 3%
- 7%
- 8%
- 10%
- 16%
【解答&解説】
湿度が同じD・E・F班は、接触時間が長くなるほど感染確率が高くなっています。A・C班も同様です。
B班はA・C班と湿度が同じなので、接触時間がA→B→C班と長くなるにつれて、感染確率も7→?→15%と高くなると推測されます。
7と15の間の数字は10%・・・(答)だけです。
3:算出式
算出式は、いくつかの項目を使って、「?」の算出式が作れるものです。難易度はかなり高めです。
【例題】
ある製造会社で、機械の出荷について工場別のデータをまとめています。
<工場別データ>
| A工場 | B工場 | C工場 | D工場 | E工場 | |
|---|---|---|---|---|---|
| 出荷量[キロリットル] | 120 | 820 | 640 | 530 | 380 |
| 出荷額[百万円] | 72 | 492 | 384 | 318 | ? |
| 正社員の数[人] | 30 | 63 | 44 | 35 | 30 |
| アルバイトの数[人] | 38 | 75 | 45 | 43 | 41 |
E工場の出荷額はいくらと推測できるか。
- 135百万円
- 185百万円
- 228百万円
- 272百万円
- 315百万円
【解答&解説】
「出荷量×0.6=出荷額」の法則を見つけられるかどうかです。
例えば、C工場の出荷量=640、出荷額=384ですが、640×0.6=384が成り立っていることがわかります。
よって、E工場の出荷額は380×0.6=228[百万円]・・・(答)となります。
🔽 本にも載ってない極秘情報 🔽
4:推移
推移は、「何人増えるごとに、何円増える」といった、増減の推移に法則があるものです。
【例題】
1年間の講座の会員数を集計しています。
| 2005年 | 2006年 | 2007年 | 2008年 | 2009年 | |
|---|---|---|---|---|---|
| 新規の講座数(講座) | 14 | 17 | 10 | 7 | 13 |
| 廃止の講座数(講座) | 4 | 9 | 5 | 3 | 6 |
| 全講座の会員数合計(人) | 420 | 465 | 360 | 315 | ? |
2009年の全講座の会員数合計は何人と推測できるか。
- 350人
- 365人
- 386人
- 405人
- 455人
【解答&解説】
2006年は新規の講座数が3講座増えて、45人増えています。
反対に2008年は新規の講座数が3講座減って、45人減っています。
ここから、新規の講座が1講座増えるごとに、全講座の会員数合計が15人増えると推測できます。
よって、2009年の増加人数=(13-7)×15=90[人]となります。
以上より、2009年の全講座の会員数合計=315+90=405[人]・・・(答)と推測できます。
5:合計が同じ
いくつかの項目の合計が、いつも同じ値になるものです。難易度は比較的低めです。
【例題】
ある広告代理店で、車の購入者に対して、購入の決め手となった広告等についてアンケートをとっています。
<単位:人>
| 車種A | 車種B | 車種C | 車種D | 車種E | |
|---|---|---|---|---|---|
| 新聞折込チラシ | 30 | 30 | 31 | 31 | 29 |
| 専門誌 | 35 | 33 | 36 | 32 | 36 |
| CM | 63 | 85 | 46 | 57 | 38 |
| DM | 3 | 4 | 0 | 0 | 3 |
| WEBサイト | 20 | 21 | 21 | 25 | 20 |
| 店頭試乗 | 67 | 45 | ? | 73 | 92 |
車種Cの店頭試乗による購入決定者数は何人と推測できるか。
- 69人
- 72人
- 76人
- 81人
- 84人
【解答&解説】
CMと店頭試乗を足すと、どの車種も130になることがわかります。
よって、求める数値は130-46=84[人]・・・(答)となります。
6:積算
積算は、個別に単価や作業量などが決まっているものです。
【例題】
ある市バスで、ある日のA〜Fルートの売上についてまとめています。
| Aルート | Bルート | Cルート | Dルート | Eルート | Fルート | |
|---|---|---|---|---|---|---|
| 大人(人) | 17 | 13 | 18 | 21 | 13 | 11 |
| 子供(人) | 5 | 6 | 5 | 3 | 10 | 4 |
| 売上金額(円) | 5,000 | 4,150 | 5,250 | 5,700 | 4,750 | ? |
大人と子供で料金はそれぞれ均一なものとするとき、Fルートの売上金額はいくらと推測できるか。
- 2,900円
- 3,100円
- 3,250円
- 3,350円
- 3,500円
【解答&解説】
各ルートの乗車人数の違いから、大人と子供のバス料金をそれぞれ求めてみます。
A・Cルートの違いは大人1人で、売上金額の違いは250円です。
B・Eルートの違いは子供4人で売上金額の違いは600円です。よって、子供1人あたり150円であることがわかります。
よって、答えは250×11+150×4=3,350[円]・・・(答)となります。
7:列ごとに計算
列ごとに計算は、その名の通り列ごとに計算することで答えを求める問題です。
例えば、「ある項目の値の2倍が、他の項目の値と同じになる」といった法則を見つけることができます。
【例題】
あるアパレルショップで、福袋の料金を検討しています。
| 福袋A | 福袋B | 福袋C | 福袋D | 福袋E | 福袋F | |
|---|---|---|---|---|---|---|
| コート(枚) | 1 | 0 | 0 | 1 | 1 | 1 |
| ワンピース(枚) | 0 | 1 | 1 | 2 | 1 | 1 |
| トップス(枚) | 0 | 0 | 1 | 0 | 1 | 1 |
| スカート(枚) | 0 | 0 | 0 | 0 | 0 | 1 |
| 料金(円) | 12,000 | 6,000 | ? | 24,000 | 21,000 | 25,000 |
福袋Cの料金はいくらと推測できるか。
- 9,000円
- 11,000円
- 14,000円
- 18,000円
- 23,000円
【解答&解説】
福袋Eから福袋Aを引くと、福袋の内訳が福袋Cと同じになります。
内訳が同じということは、金額も同じです。
よって、答えは21,000-12,000=9,000[円]・・・(答)となります。
🔽 本にも載ってない極秘情報 🔽
四則逆算
四則逆算は計算式の中に含まれている□に入る数を求める問題です。
玉手箱の四則逆算では以下5パターンの問題が用意されています。
- 整数
- 小数
- 分数
- パーセント(%)
- □が複数個存在
それぞれの例題は以下です。
1:整数
【例題】
□に入る数値として正しいものを選択肢の中から1つ選びなさい。
□-4672=8204
- 14026
- 3532
- 10764
- 423
- 12876
【解答&解説】
□=8204+4672=12876・・・(答)となります。
2:小数
【例題】
□に入る数値として正しいものを選択肢の中から1つ選びなさい。
0.16×□=0.4×0.4
- 0.01
- 0.1
- 1
- 10
- 100
【解答&解説】
□=(0.4×0.4)÷0.16=1・・・(答)となります。
3:分数
□に入る数値として正しいものを選択肢の中から1つ選びなさい。
□ × 1/3 ÷ 8=24-9
- 360
- 792
- 40
- 15
- 144
【解答&解説】
□=(24-9)×8×3=15×8×3=360・・・(答)となります。
4:パーセント(%)
【例題】
□に入る数値として正しいものを選択肢の中から1つ選びなさい。
120の□%=28.8
- 6.125
- 12
- 18
- 24
- 32.35
【解答&解説】
120×□÷100=28.8ということなので、□=28.8×100÷120=24・・・(答)となります。
5:□が複数個存在
□に入る数値として正しいものを選択肢の中から1つ選びなさい。ただし、□には同じ値が入るものとする。
□×12+□×6=54
- 7
- 6
- 5
- 4
- 3
【解答&解説】
□×12+□×6=54
⇔ □×18=54
なので、□=54÷18=3・・・(答)となります。
※もっとたくさんの例題を解きたい人は「玉手箱の四則逆算・四則演算とは?練習問題とコツ!時間足りない人は?ボーダーは?」をぜひご覧ください。
🔽 本にも載ってない極秘情報 🔽
玉手箱の計数理解(非言語・数学)のコツ
玉手箱の計数の問題例がわかったところで、ここからは、玉手箱の計数の問題を解くためのコツについて解説していきます。
図表の読み取り
図表の読み取りのコツは以下の3つです。
- わからない問題は時間をかけずに勘で回答する
- 余計な情報に惑わされないようにする
- 問題を解くために必要な公式を覚える
それぞれの詳細は以下です。
わからない問題は時間をかけずに勘で回答する
玉手箱の図表の読み取りは序盤の問題が易しめで、後半になるにつれて難易度が上がっていきます。
図表の読み取りは1問あたりに使える時間がかなり短いので、時間配分が非常に重要です。
玉手箱は正解した問題の数のみで採点が行われます(=誤謬率が計測されない)
なので、わからない問題は時間をかけず、即座に勘で回答して次の問題に進むのが得策です。
※詳しくは「玉手箱で誤謬率は計測されない!わからない問題は適当に埋めるでOK!」をご覧ください。
余計な情報に惑わされないようにする
図表の読み取りで出題される図や表・グラフにはたくさんの情報が記載されています。
しかし、問題を解くために必要な情報はその中のほんの一部にしかすぎません。
なので、図表の読み取りでは問題を解くために本当に必要な情報を即座に見極める能力が必要です。
問題文に登場する項目名や年度などを手がかりにして必要な数値を素早く拾い、それらの数値は見失わないようにメモを取る、数値にマウスを合わせるなどの工夫をしましょう。
問題を解くために必要な公式を覚える
図表の読み取り問題を解くためには知っておかなければならない数学(算数)の公式があります。
それは以下の3つです。
- 「は」÷「の」の法則
- 増加率・減少率の求め方
- 内項の積=外項の積
それぞれの公式の詳細は「玉手箱の図表の読み取りとは?ボーダーやコツは?時間足りない場合は?練習問題付き」で解説しているので、ぜひ参考にしてください。
🔽 本にも載ってない極秘情報 🔽
表の空欄の推測
表の空欄の推測のコツは主に以下の2つです。
- 空欄の項目と連動する項目を見つける
- 計算しやすい数値を使う
それぞれの詳細は以下です。
空欄の項目と連動する項目を見つける
表の空欄の推測では多くの列・行が存在しますが、答えを導くのに必要な項目は一部であることが多いです。
なので、空欄の項目の値に関係がある項目を素早く見つけることが重要となります。
関係がある項目を見つける方法として王道なのは、空欄の項目を小さい順に見ていき、同じ順番になる項目を探すというものです(上記でご紹介した「大小」の例題など)
表の空欄の推測が難しいと感じる人は、まずは上記を疑ってみることをおすすめします。
計算しやすい数値を使う
表の中には法則性を見つけやすいキリのいい数字が用意されていることが多いです。
表の空欄の推測ではこのような数字を見つけて上手く活用できると時間短縮に繋がります。
キリのいい数字の見つけ方は数字の下3〜4桁に注目することです。
※詳細は「玉手箱:表の空欄の推測とは?できない人続出!何割必要?導入企業は?難しいのでコツが必要です」で解説しているので、ぜひ参考にしてください。
意外と便利なテクニックなので、玉手箱を受検予定の就活生や転職活動中の社会人はぜひ知っておきましょう。
四則演算
玉手箱の四則逆算のコツは以下の4つです。
- 序盤の問題は時間をかけずに解く
- 割り切れる分数は小数に変換する
- 11×11〜19×19、25×25の計算結果を暗記する
- 混乱した場合は勘で回答して次の問題に進む
それぞれの詳細は以下です。
序盤の問題は時間をかけずに解く
玉手箱の四則逆算は序盤の問題であるほど簡単です。
なので、序盤の問題はなるべく時間をかけずにサクッと解きたいところです。
そのためにも電卓を普段から使うようにして、電卓に慣れておきましょう。
使いやすい電卓を持っていない場合は新たに電卓を買い直すことをおすすめします。
おすすめの電卓は後ほどご紹介するので、ぜひ参考にしてください。
割り切れる分数は小数に変換する
式に含まれる分数が割り切れる場合は「分子÷分母」の計算をして小数に変換することをおすすめします。
逆に、式に含まれる分数が割り切れない場合は分数のまま計算するしかありません。
ちなみにですが、分母が2、4、5、8、10、16、20ならその分数は必ず割り切れます(分母が20以下の場合)
3/4=0.75、1/16=0.0625など、できるだけ暗記しておくと便利です。
11×11〜19×19までの計算結果を暗記する
□が複数個存在する問題で多いですが、計算をしていくと□×□=225などの形になることがあります。
以上の場合は□=15ですが、11×11〜19×19までの計算結果を暗記しておくと一瞬で□=15が導けます。
玉手箱の四則逆算を受検予定の人は必ず暗記しておきましょう。11×11〜19×19までの計算結果は以下です。
- 11×11=121
- 12×12=144
- 13×13=169
- 14×14=196
- 15×15=225
- 16×16=256
- 17×17=289
- 18×18=324
- 19×19=361
ちなみにですが、25×25=625です。これも暗記しておくと便利です。
混乱した場合は勘で回答して次の問題に進む
上記でも解説した通り、玉手箱は誤謬率が計測されないWEBテスト(適性検査)です。
なので、わからない問題に遭遇したときはさっさと勘で回答して次の問題に進むのが賢明です。
特に玉手箱の四則逆算は試験時間が短いので、頭が混乱してわからない問題にいつまでも時間を使わないようにしましょう。
🔽 本にも載ってない極秘情報 🔽
玉手箱の計数が終わらない人がやるべきこと
上記でも解説した通り、玉手箱の計数は
- 図表の読み取り(35分で40問または15分で29問)
- 表の空欄の推測(35分で35問または20分で20問)
- 四則逆算(9分で50問)
なので、問題数に対して試験時間がかなり短いです。
ほとんどの受検者はすべての問題を解き終えることができずに試験終了となります。
しかし、それは至って普通のことなのでご安心ください。
そもそもですが、玉手箱の計数ではすべての問題を解こうとしなくても大丈夫です。
玉手箱は比較的難しいWEBテスト(適性検査)なので、多くの企業はボーダーラインを4〜5割程度に設定しています。
※詳しくは「玉手箱のボーダー・合格ラインは?正答率目安・何割取ればOK?コンサル業界・中途は?」をご覧ください。
つまり、多くの玉手箱受検者にとっては全部の問題を無理に解こうとせず、用意された問題の7〜8割程度の中でどれだけ点数を取れるかが重要です。
無理にすべての問題を解こうとして焦ってしまい、その結果として正答率が下がってしまっては本末転倒です。
また、玉手箱に限らずですが、WEBテスト(適性検査)の受検者の中にはわからない問題(=解法が思い浮かばない問題)に対して多くの時間を使ってしまう人もいます。
玉手箱は特に試験時間が短いので、わからない問題は即座に勘で回答し、次の問題に移るようにしましょう。
繰り返しにはなりますが、玉手箱では誤謬率が計測されないので、わからない問題はさっさと勘で回答するのが得策です。
玉手箱を受検予定の就活生や転職活動中の社会人は、上記の前提を頭に入れて計数の問題を解くようにしてください。
※「玉手箱が解き終わらない・全部解けない人がやるべきことは?計数・英語・四則逆算など科目別に解説」もぜひ合わせてご覧ください。
玉手箱の計数には解答集・答えがあるって本当?
玉手箱の計数には解答集(答え)があるという噂を聞いたことがある人もいるでしょう。
解答集とはWEBテストの答えが掲載された以下のようなエクセルやGoogle SpreadSheetのことです。

結論から言うと、玉手箱の解答集は存在します。
※「玉手箱解答集・答え2027卒は無料である?バレる?エクセルの使い方は?noteで売ってる?」もぜひ参考にしてください。
Googleやnoteなどで「玉手箱 解答集」と検索すると、解答集を販売している人を見つけることが可能です。
しかし、玉手箱を開発している日本エス・エイチ・エル株式会社は解答集の存在をもちろん把握しています。
なので、玉手箱では定期的に新しいが問題を追加されたり、選択肢の順番を入れ替えるなどの対策が取られています。
解答集では問題の解答しか掲載されていない(解き方は掲載されていない)ので、かなり信憑性が低くおすすめできません。
また、解答集を利用して逮捕・起訴された事例はありませんが、法的にはかなりのグレーゾーンです。
ちなみにですが、2022年11月には就活中の女子大生のWEBテスト(適性検査)を代行した男性が逮捕・起訴されるという事件が発生しています。
※事件の詳細は「玉手箱の代行は犯罪!逮捕者も出ているので絶対にやめておきましょう」をご覧ください。
警視庁や検察官は解答集の存在を把握している可能性が高いため、解答集を利用するのはかなり危険です。絶対に利用しないようにしましょう。
ちなみにですが、玉手箱にはたった3時間の勉強で玉手箱が通過してしまう勉強法があります。
これさえあれば解答集なんて必要ありません。限りなく少ない努力で内定に大きく近づきます。
これは私が100回以上もの玉手箱受検を通して生み出した、どの本にも載っていない超コスパの良い究極の勉強法です。
興味のある人はぜひ以下のボタンからその方法をチェックしてみてください。
玉手箱の計数は何割取ればいい?
先ほども解説しましたが、玉手箱のボーダーは4〜5割程度に設定されているケースが多いです。
※外資系コンサルティング企業や外資系金融企業など、就職・転職難易度が高い企業はボーダーラインを8割など高めに設定している可能性もありますのでご注意ください。
なので、例えば図表の読み取り(35分・40問)で4割を取ろうと思うと、40×0.4=16[問]の正解数が必要となります。
表の空欄の推測に関しても同様です。
ただし、四則逆算は注意が必要です。四則逆算は問題数=50問なので、単純計算すると
- 4割の場合:50×0.4=20[問]
- 5割の場合:50×0.5=25[問]
ですが、四則逆算は試験時間がかなりタイトなだけで、問題自体は上記でご紹介した例題の通りかなり簡単です。
なので、四則逆算は4〜5割程度の得点だと物足りなく、6割程度(問題数でいうと50×0.6=30[問])の得点は欲しいところです。
「玉手箱は4割で通過する?4割取るためのポイントを科目別に解説」という記事もご用意しているので、ぜひ参考にしてください。
玉手箱の計数で電卓は使える?
玉手箱の計数で電卓が使えるかどうかは受検方式によって異なります。
玉手箱には以下3つの受検方式が存在します。
- 自宅受検型
- C-GAB
- C-GAB plus
※それぞれの詳細を知りたい人は「玉手箱方式とは?3つの受検方式と例題をすべて紹介!」をご覧ください。
このうち、電卓の使用が許可されているのは自宅受検型の玉手箱のみです。計算用紙とペンの使用も許可されています。
C-GABとC-GAB plusの玉手箱では電卓の使用が禁止されていますのでご注意ください(計算用紙とペンの使用は許可されています)
ちなみにですが、C-GABは自宅ではなく専用の試験会場(テストセンター)で玉手箱を受検する方式のことです。
※テストセンターの詳細は「玉手箱のテストセンターとは?47分?電卓は?会場予約や導入企業・問題例・服装について解説」をご覧ください。
計算用紙とペンは試験会場にいるスタッフから配布されたもののみ使用可能です。
カンニングなどの不正行為防止の観点から、自分で持参した計算用紙とペンを使用することはできません。
玉手箱と電卓の関係については「玉手箱は電卓・計算機禁止?おすすめは?スマホ電卓はなし?自宅受検はあり?」で詳しく解説しているので、気になる人はぜひ参考にしてください。
🔽 本にも載ってない極秘情報 🔽
玉手箱の計数の練習問題
最後に、計数の練習問題をご用意しました。
どれも本番の玉手箱の計数で出題される問題の難易度に近い問題なので、玉手箱を受検予定の就活生や転職活動中の社会人はぜひ解いてみてください。
【練習問題1】
以下の表を見て問いに答えなさい。
<株式会社Aの推移>
| 年 | 売上額[百万円] | 社員数[人] | 拠点数[件] |
|---|---|---|---|
| 2001 | 9,742,429 | 239,026 | 2,849 |
| 2002 | 11,906,104 | 250,728 | 3,050 |
| 2003 | 13,349,902 | 269,308 | 3,104 |
| 2004 | 12,827,727 | 234,724 | 2,496 |
| 2005 | 13,391,402 | 229,011 | 2,590 |
| 2006 | 8,303,900 | 226,683 | 2,921 |
| 2007 | 10,329,045 | 240,592 | 3,201 |
| 2008 | 13,840,201 | 284,204 | 3,104 |
2004年における1拠点あたりの社員数の平均は、2002年における1拠点あたりの社員数の平均よりも約何人増加したか。最も近いものを以下の選択肢の中から1つ選びなさい。
- 8.3人
- 9.9人
- 10.6人
- 11.8人
- 12.5人
【解答&解説】
- 2004年における1拠点あたりの社員数の平均=234,724÷2,496≒94.04[人]
- 2002年における1拠点あたりの社員数の平均=250,728÷3,050≒82.20[人]
より、94.04-82.20=11.84となるので、正解は11.8人・・・(答)です。
【練習問題2】
あるネットショップで、新作ゲームの発売前予約数と発売後2ヶ月間の販売数を集計しています。
<新作ゲームの販売状況>
| ゲームA | ゲームB | ゲームC | ゲームD | ゲームE | |
|---|---|---|---|---|---|
| 発売前予約数[個] | 138 | 29 | 183 | 1,337 | 364 |
| 販売数[個/発売後2ヶ月] | 19,320 | 4,060 | 25,620 | 187,180 | ? |
ゲームEの発売後2ヶ月の販売数は何個と推測できるか。
- 36,400個
- 43,180個
- 47,320個
- 50,960個
- 54,600個
【解答&解説】
「発売前予約数×140=販売数」という式が成り立っています。
例えば、ゲームAは138×140=19,320、ゲームBは29×140=4,060になっています。
よって、正解は364×140=50,960[個]・・・(答)です。
【練習問題3】
□に入る数値として正しいものを選択肢の中から1つ選びなさい。
(1)□×3=81÷6
- 13.5
- 4.5
- 45
- 7.5
- 5.25
(2)1/5 ÷ (0.75-□)=1 ÷ 1/4
- 0.25
- 0.7
- 0.1
- 0.15
- 0.95
(3)540の□%=97.2
- 12
- 14
- 18
- 21
- 23
(4)22×8=(□×12-□)×2
※□には同じ値が入ります。
- 12.5
- 8
- 32
- 4
- 16
【解答&解説】
(1)□=(81÷6)÷3=13.5÷3=4.5・・・(答)です。
(2)与式 ⇔ 1/5 ÷ (0.75-□)=4 ⇔ 1/5 ÷4 = 0.75-□ ⇔ 1/20 = 0.75-□より、□=0.75 – 1/20=0.75-0.05=0.7・・・(答)となります。
(3)540×□÷100=97.2より、□=(97.2×100)÷540=9720÷540=18・・・(答)となります。
(4)与式 ⇔ 22×8÷2=□×12-□ ⇔ 88=11×□より、□=88÷11=8・・・(答)です。
🔽 本にも載ってない極秘情報 🔽
今回は玉手箱の計数理解(非言語・数学)の例題を使いながら問題の解き方のコツや、終わらない人がやるべきことなどについて解説していきました。
玉手箱の計数は制限時間がかなり短いので、多くの受検者が苦戦します。
玉手箱の計数は言語よりも入念に勉強・対策をしておきましょう。


