
WEBテスト(適性検査)の一種である玉手箱では図形問題が出題される・試験時間は12分または16分であるという噂がありますが、完全な嘘なのでご注意ください。
後ほど詳しく解説しますが、玉手箱で図形問題が出題されることはありません。
※「玉手箱とは?対策方法や試験の特徴は?対策いらない?完全解説で就活生・社会人必見!」もぜひ参考にしてください。
本記事では玉手箱を今までに100回以上受検し、日本一玉手箱を熟知している私アキラが、玉手箱と図形問題の関係について徹底解説していきます。
玉手箱を受検予定の就活生や転職活動中の社会人はぜひ参考にしてください。
ちなみにですが、玉手箱にはたった3時間の勉強で玉手箱が通過してしまう勉強法があります。
これさえあれば限りなく少ない努力で内定に大きく近づきます。
これは私が100回以上もの玉手箱受検を通して生み出した、どの本にも載っていない超コスパの良い究極の勉強法です。
興味のある人はぜひ以下のボタンからその方法をチェックしてみてください。
玉手箱で図形問題は出る?12分・16分の噂は?
冒頭でも解説した通り、玉手箱で図形問題が出題されることは絶対にありません。
玉手箱の計数の出題範囲は以下の通りとなっており、図形問題は出題範囲に含まれていません。
※「玉手箱の計数理解(非言語・数学)のコツ!終わらない人続出?例題・練習問題と解答付き!」もぜひ参考にしてください。
| 科目 | 試験時間 | 問題数 |
|---|---|---|
| 四則逆算 | 9分 | 50問 |
| 図表の読み取り | 35分または15分 | 40問または29問 |
| 表の空欄の推測 | 35分または20分 | 35問または20問 |
それぞれの例題は以下です。図形が登場することはありません。
【四則逆算の例題】
□に入る数値を以下の選択肢から選びなさい。
(□+15)×14=280
- 5
- 6
- 7
- 8
- 9
【解答&解説】
□=(280÷14)-15=20-15=5・・・(答)となります。
※「玉手箱の四則逆算・四則演算とは?練習問題とコツ!時間足りない人は?ボーダーは?」もぜひ合わせてご覧ください。
【図表の読み取りの例題】
表を見て次の問いに答えなさい。
<SNS上でのトラブル経験の有無(年代別)>
| 年代 | トラブルにあったことはない | トラブルにあったことがある |
|---|---|---|
| 60代以上 | 93.5% | 6.5% |
| 50代 | 90.4% | 9.6% |
| 40代 | 85.9% | 14.1% |
| 30代 | 87.9% | 12.1% |
| 20代以下 | 74.0% | 26.0% |
SNS上でのトラブル経験がある20代以下の割合は、同40代の割合の何倍か。もっとも近いものを以下の選択肢の中から1つ選びなさい。
- 0.38倍
- 1.23倍
- 1.84倍
- 2.71倍
- 3.56倍
【解答&解説】
SNS上でのトラブル経験がある20代以下の割合は表より26.0%です。
同40代の割合は表より14.1%です。
26.0÷14.1=1.843・・・となるので、正解は1.84倍・・・(答)です。
※「玉手箱の図表の読み取りとは?ボーダーやコツは?時間足りない場合は?練習問題付き」もぜひ参考にしてください。
🔽 本にも載ってない極秘情報 🔽
【表の空欄の推測の例題】
ある食品メーカーで、清涼飲料水類の月ごとの売上と気温の関係をまとめている。
<月別売上と気温>
| 6月 | 7月 | 8月 | 9月 | 10月 | 11月 | |
|---|---|---|---|---|---|---|
| 平均最高気温[℃] | 24 | 27 | 31 | 32 | 28 | 23 |
| 平均最低気温[℃] | 17 | 20 | 23 | 25 | 21 | 15 |
| 月間売上[万円] | 15,300 | 16,500 | 18,100 | ? | 16,900 | 14,900 |
9月の月間売上はいくらと推測できるか。
- 17,900万円
- 18,300万円
- 18,500万円
- 18,600万円
- 18,800万円
【解答&解説】
平均最高気温が1℃上下するごとに、月間売上は400万円上下することがわかります。
例えば、6月から7月にかけては平均最高気温が27-24=3[℃]上昇しています。
よって、7月の月間売上は15,300+400×3=15,300+1,200=16,500[円]になっています。
8月から9月にかけては平均最高気温が32-31=1[℃]上昇しているので、9月の月間売上=18,100+400×1=18,500[万円]・・・(答)となります。
※「玉手箱:表の空欄の推測とは?できない人続出!何割必要?導入企業は?難しいのでコツが必要です」もぜひ合わせてご覧ください。
図形問題が出題されるWEBテスト(適性検査)は?
玉手箱で図形問題が出題されないことはお分かりいただけたかと思いますが、図形問題が出題されるWEBテスト(適性検査)は何か気になっている人もいるのではないでしょうか?
※「玉手箱とWEBテスト・適性検査の違いとは?対策方法や例題・問題集もご紹介!」もぜひ参考にしてください。
結論から申し上げますと、TG-WEBとCUBICでは図形問題が出題される可能性があります。
特にTG-WEBは数多くあるWEBテスト(適性検査)の中で最も難しいと言われているので事前の対策は必須です。
※TG-WEBの詳細は「TG-WEBのすべてがわかるサイト」にまとまっているので、ぜひ参考にしてください。
TG-WEBとCUBICで出題される図形問題の例題はそれぞれ以下の通りです。
【TG-WEBの例題】
面積が20cm2の正三角形を、次の図のように、底辺の半分が重なるようにしながら並べていく。40枚の正三角形を並べてできる図形の面積として正しいのはどれか。
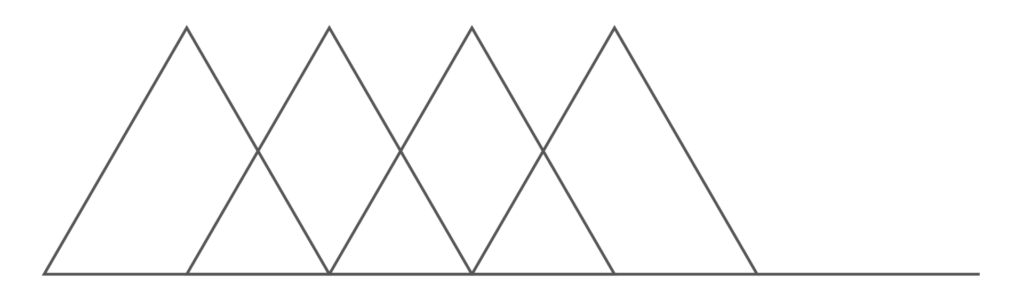
- 550cm2
- 575cm2
- 585cm2
- 595cm2
- 605cm2
【解答&解説】
正三角形を1枚目から順に並べて合計の面積を計算します。
まず、1枚目は20cm2ですが、2枚目は、1枚目と、以下の図の色の付いた部分が重なります。
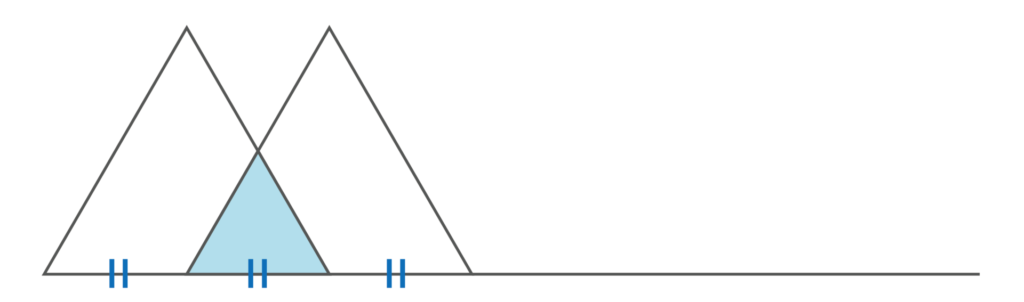
この色の付いた部分も正三角形で、1辺の長さは元の正三角形の半分(1/2)なので、面積は1/4となり、20cm2 × 1/4=5cm2と分かります。
すると、1枚目に2枚目から順に重ねることで、以下の図のように、面積は20-5=15[cm2]ずつ増えていくことになります。
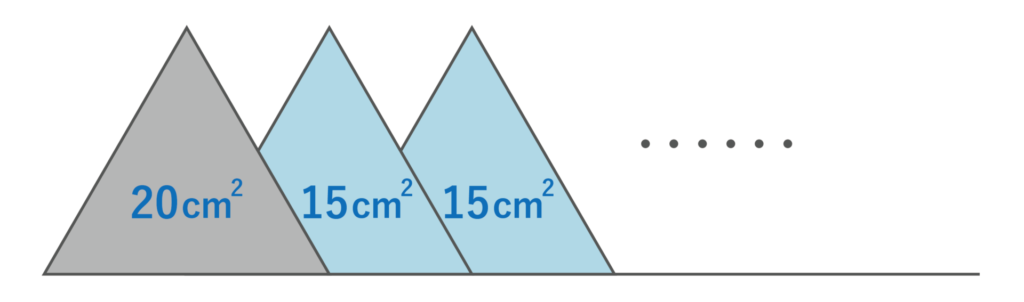
以上より、40枚並べてできる図形の面積は、20+15×39=605[cm2]となり、5・・・(答)が正解です。
【CUBICの例題】
以下の図は、一辺の長さが9cmの正方形ABCDである。点E、FはそれぞれAB、CD上にあり、辺AD、辺EF、辺BCは並行である。また、点Gは辺AD上にあり、GD=DFである。台形GEFDの面積が18cm2であるとき、線分GDの長さは以下の選択肢のうちどれか。
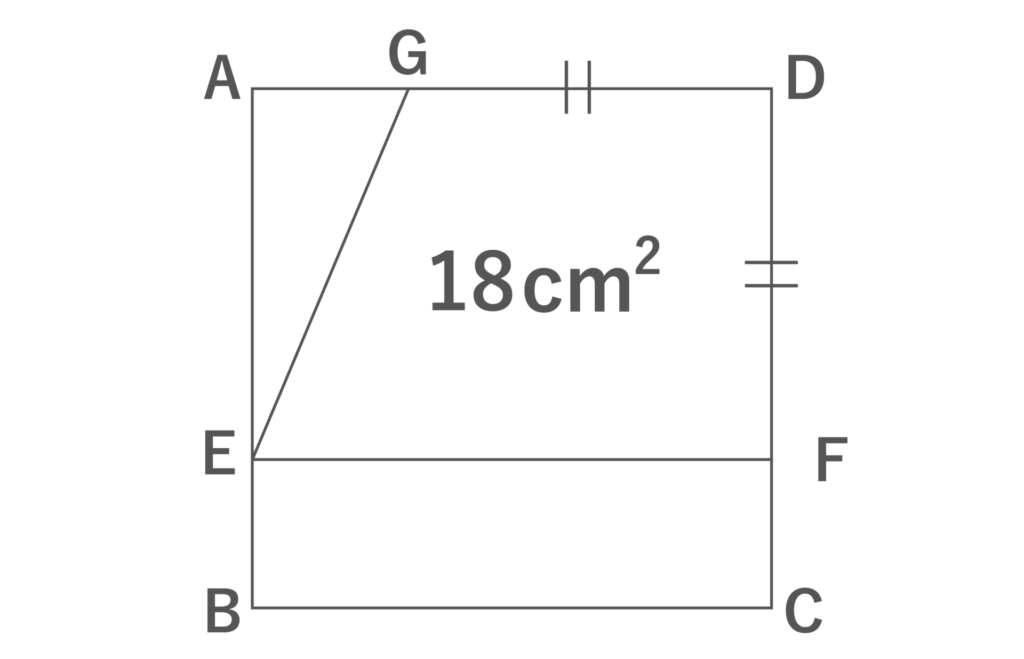
- 2.0cm
- 2.5cm
- 3.0cm
- 3.2cm
- 3.5cm
- 4.2cm
【解答&解説】
線分GDの長さをA[cm]とおきます。
すると、(A+9)× A ÷ 2=18という方程式が立てられるので、これを整理するとA2+9A-36=0となります。
※台形の面積は「(上底+下底)× 高さ ÷ 2」で計算可能です。
A2+9x-36を因数分解すると(A+12)(A-3)となるので、A=-12、3です。
Aは線分の長さなので、マイナスの数はあり得ません。よって、A=3[cm]となるので、正解は3・・・(答)です。
🔽 本にも載ってない極秘情報 🔽
今回は玉手箱で図形問題は出題されるのかについて解説しました。
玉手箱に限らずですが、WEBテスト(適性検査)を受検予定の人は自分が受検するWEBテストの出題範囲を正確に把握した上で勉強・対策を行いましょう。


